Introduction to Location Estimates in Statistics
Location estimates, also known as measures of central tendency, play a vital role in the field of statistics. They help us summarize and understand the central value of a dataset. In this article, we’ll dive deep into the world of location estimates, exploring different types, their importance, how to calculate them, and their limitations.
Statistics for Data Scientists
Peter Bruce’s “Practical Statistics for Data Scientists” is an essential and accessible guide for anyone delving into the realm of data science. The book effectively simplifies complex statistical concepts and presents them in an easy-to-understand manner. With its practical examples and clear explanations, it serves as a valuable resource for both beginners and experienced data scientists alike.
Types of Location Estimates
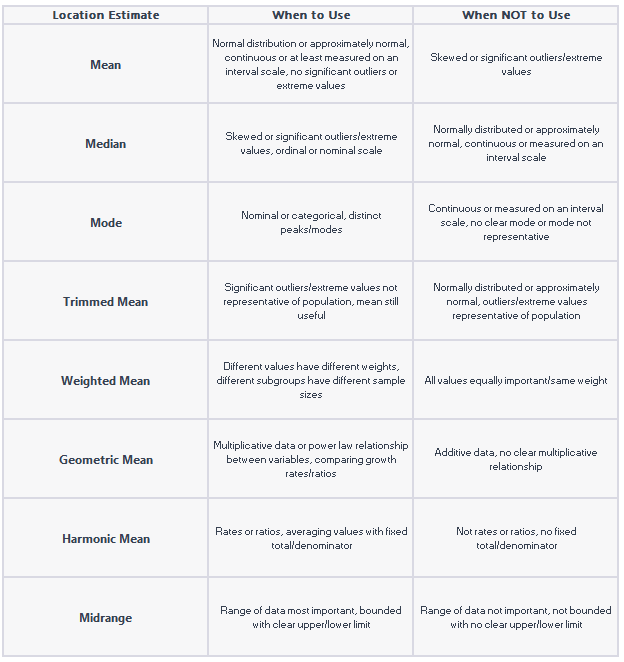
There are three main types of location estimates: mean, median, and mode. Each type has its own unique properties and applications.
1. Mean
The mean, also known as the average, is the sum of all values in a dataset divided by the total number of values. It’s a commonly used location estimate, as it provides a straightforward way to summarize the center of a dataset.
2. Median
The median represents the middle value in a dataset when all values are arranged in ascending or descending order. If the dataset has an odd number of values, the median is the middle value. If the dataset has an even number of values, the median is the average of the two middle values.
3. Mode
The mode is the value that occurs most frequently in a dataset. It’s possible for a dataset to have multiple modes or no mode at all if no value is repeated.
Importance of Location Estimates
Location estimates provide critical insights into various aspects of a dataset, such as understanding central tendencies, decision-making, and outlier detection.
1. Understanding Central Tendencies
Location estimates give us a sense of where the central tendency of a dataset lies. This helps in summarizing the data, making it easier to understand and interpret. Having a clear picture of the central tendency allows us to make comparisons between different datasets or identify trends over time.
2. Decision Making
In many fields, such as business, economics, and social sciences, location estimates play a crucial role in decision-making processes. By understanding the central value of a dataset, decision-makers can make informed choices based on the data.
3. Outlier Detection
Location estimates can also be used to detect outliers in a dataset. Outliers are data points that significantly deviate from the central value. Identifying and understanding outliers can help improve the quality of data analysis and lead to more accurate conclusions.
Calculating Location Estimates
1. Arithmetic Mean
To calculate the arithmetic mean, simply add all values in a dataset and divide the sum by the total number of values.
2. Weighted Mean
The weighted mean takes into account the importance or frequency of each value in a dataset. To calculate the weighted mean, multiply each value by its corresponding weight, sum the products, and then divide by the sum of the weights.
3. Median and Mode Calculation
To find the median, arrange the values in ascending order and identify the middle value(s) as described earlier. For the mode, simply determine the value(s) that occur most frequently in the dataset.
Choosing the Appropriate Location Estimate
When analyzing a dataset, it’s essential to choose the right location estimate based on the data’s characteristics and the purpose of your analysis.
Considerations for Mean, Median, and Mode
Use the mean when you need a precise measure of central tendency and the dataset is not heavily affected by outliers or extreme values.
The median is a better choice when the dataset is skewed or has extreme values that could distort the mean.
The mode is most suitable for categorical or discrete data, where determining the most frequent value is more relevant than calculating the average or the middle value.
Limitations of Location Estimates
While location estimates are incredibly useful, they have certain limitations:
Skewness and Kurtosis
The mean is sensitive to skewness and kurtosis, which can affect the accuracy of the estimate. Skewness refers to the asymmetry of the data distribution, while kurtosis measures the “tailedness” of the distribution. In such cases, the median or mode might be more appropriate.
Conclusion
Mastering location estimates in statistics involves understanding the different types, their importance, and how to calculate them. It also requires knowing when to use each estimate based on the data’s characteristics and the purpose of your analysis. With this knowledge, you’ll be well-equipped to analyze and interpret various datasets, make informed decisions, and detect outliers effectively.
Frequently Asked Questions
1. What is the main difference between mean, median, and mode?
The mean is the average of all values in a dataset, the median is the middle value when the data is arranged in ascending or descending order, and the mode is the most frequently occurring value.
2. When should I use the median instead of the mean?
The median is preferred when the dataset is skewed or has extreme values that could distort the mean.
3. Can a dataset have multiple modes or no mode at all?
Yes, a dataset can have multiple modes if more than one value occurs with the same highest frequency. It can also have no mode if no value is repeated.
4. What are the limitations of location estimates?
Location estimates can be sensitive to skewness and kurtosis, which can affect the accuracy of the estimate. In such cases, choosing the right location estimate based on the data’s characteristics and the purpose of your analysis is crucial.
5. How can location estimates help in decision-making processes?
By understanding the central value of a dataset, decision-makers can make informed choices based on the data. Location estimates provide a way to summarize and interpret the data, making it easier to compare different datasets or identify trends over time, ultimately aiding in the decision-making process.
🐼.